一些 dp 的优化方式

算法笔记
决策单调性, 动态规划, 带权二分, 斜率优化

简单总结了一下

决策单调性

一些时候 dp 转移方程是这个样子

这个时候暴力是 $O(n^2)$ 的。如果 $w(i, j)$ 满足一些特殊的性质，那么就可以优化他了。

决策单调性：

对于 $i$ ，他的决策 $opt(i)$ 就是所有的 $j$ 中使得转移式子达到最值的那个 $j$ 。

如果对于任意的 $i, j$ 使得 $i \leq j$ 都有 $opt(i) \leq opt(j)$ 那么就有决策单调性。 它的用处放到后面。

四边形不等式： 如果对于任意的 $1 \leq a \leq b \leq c \leq d \leq n$ 都有 $w(a, c) + w(b, d) \leq w(a, d) + w(b, c)$ ，那么 $w$ 就满足四边形不等式。

一个重要的事情是：如果 $w$ 满足四边形不等式，那么就有决策单调性

一个好理解的证明方式：如果没有决策单调性，那么我们可以找到不降的四个数 $a, b, c, d$ ，这四个点满足 $a = opt(d), b = opt(c)$ 即 $a, b$ 分别是 $c, d$ 的决策点。由于不满足决策单调性所以肯定能找到。此时 $dp_c + dp_d = dp_i + dp_j + w(a, d) + w(b, c)$ 。如果我们把决策点互换，即让 $b = opt(d), a = opt(c)$ ，此时 $dp_c + dp_d = dp_i + dp_j + w(a, c) + w(b, d)$ 。由于满足四边形不等式，下面的总和根据定义一定 $ \leq $ 上面的总和。就能推出决策点交换后 $c, d$ 至少有一个要更优。所以他是满足决策单调性的。（不是很严谨）

如果看到一个题，dp式子长成上面那个样子，没有什么很好的办法搞，就要考虑决策单调性。一般都是满足四边形不等式，不放心就证一下。

有了决策单调性，然后该如何优化？

再先看一个问题：给定一个 $n * n$ 表格，告诉你每行的最小值所在的列是单调不减的，找出每行每列的最小值及其所在的位置。

对于这个问题，我们可以利用分治来解决。用 solve(l, r, L, R) 来求解行在 $[l, r]$ 中列在 $[L, R]$ 中的子问题。每次我找到最中间的行 $mid$，暴力从 L 到 R for 找出最小值的列 $pos$，然后由于最小值位置不减，分成 solve(l, mid - 1, L, pos) 和 solve(mid + 1, r, pos, R) 继续求解。这样做的复杂度是 $O(n \log n)$ 。

所以这和决策单调性有什么关系？如果你把最小值所在的列看成决策点所在的位置，那么是否就成功的转化成了这个问题？所以我们找出了一种 $O(n \log n)$ 的方法。代码也十分好写。

另外一种处理决策单调性的方法在例题2中出现。

[例题1] CF 321E 题面

设 $dp[i][k]$ 表示前 $i$ 个人分了 $k$ 段的最小值。

先可以写出状态转移方程

其中 $w(i, j)$ 表示把 $[j + 1, i]$ 中所有人分成一组的代价。就是一个矩阵的元素和。

由于它是矩阵的元素和，所以很显然满足四边形不等式。于是就有决策单调性。

但是有一个 $k$ 的限制。这又应该如何处理？这里可以 按层分治 。可以发现，如果有了所有的 $dp[i][k]$ ，那么通过上面的方法就可以求出所有的 $dp[i][k + 1]$。于是，预处理 $k = 1$ 的情况，然后枚举 $k$，每次分治求出下一层的信息。 复杂度 $O(n k \log n)$ 。

[例题2] NOI2009 诗人小G 题面

方程很显然。设 $dp_i$ 表示前 $i$ 句诗的最小代价。

$w(i, j) = (sum_i - sum_j - L - 1) ^ P$ (这里的 $sum_i$ 是带上空格之后的，最后的减一是末位不能加空格)。

可以证明 $w$ 满足四边形不等式。分治的做法在这里行不通了。为什么之前可以？因为他是按层分治，而这里没有这个条件，你就没法及时的得到信息了。你在找最小值的时候这个地方的数可能根本没有填上。我们考虑寻找另外的方法。

当我们一个 dp 值都没有的时候，考虑目前的 $opt(i)$ 一定是：

00000000000000000000000000000000000000000000000000000000000000000000

当我们有了第一个 $dp$ 值，那么可能有一些 opt 产生变化。由于决策单调性，所以一定变化了一个后缀比如：

00000000000000000000011111111111111111111111111111111111111111111111

然后有了第二个 $dp$ 值，会有一些 opt 变成 2 。比如

00000000000000000000011111111111111111111111111111111222222222222222

如此类推，我们试图从中找出一些性质。显然，每个决策形成一个区间。

我们考虑用一个栈来维护决策。用 $l_i$ 和 $r_i$ 来表示 $i$ 这个决策所形成的的区间的左右端点。

每次加入一个新的决策 $i$，与栈顶的决策点 $t$ 比较。有两种情况：

  1. 如果在 $l_t$ 处 $t$ 的转移没有 $i$ 的优，那么这个决策整个就没有用了。即 $i$ 会把 $t$ 这一整段区间都覆盖住。此时把栈顶弹掉，继续。
  2. 不满足上述情况，那么 $i$ 的覆盖终止于 $t$ 。此时由于决策单调性，直接二分转折点 $pos$（即这个区间在转折点前是 $t$ ，后半部分是 $i$ ）。让 $r[t] = pos - 1, l[i] = pos, r[i] = n$

这样做的复杂度是 $O(n \log n)$

这一部分的代码还有一些细节问题，我直接贴出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 注意这里的 w(i, j) 表示的是 dp[j] + 文中的 w(i, j) 
int h = 1, t = 0; l[0] = 1, r[0] = n;
Q[++t] = 0;  // 要把 0 先放进去 
for(int i = 1; i <= n; i++) {
  while(h <= t && r[Q[h]] < i) h++; // 把栈底的没用的元素弹掉。
  dp[i] = w(i, Q[h]); pre[i] = Q[h]; // 更新 dp 以及 i 处的决策点
  if(w(n, Q[t]) < w(n, i)) continue ; // 根本不会覆盖住任何一个区间直接弹掉
  while(h <= t && w(l[Q[t]], Q[t]) > w(l[Q[t]], i)) t--; // 弹掉没用的
  int lp = l[Q[t]], rp = n, pos = n; 
  while(lp <= rp) {
    int mid = (lp + rp) >> 1; 
    if(w(mid, Q[t]) > w(mid, i)) {
      pos = mid, rp = mid - 1; 
    } else lp = mid + 1; 
  } // 二分 pos 
  l[i] = pos; r[i] = n; 
  r[Q[t]] = pos - 1; Q[++t] = i; 
}

斜率优化

转移方程形如 $dp_i = \min(a[j] + b[j] + c[i] \cdot d[j])$ 。$a[i]$ 表示和 $i$ 相关的部分，其他类似。

直接用题目讲

[例题3] HNOI2008 玩具装箱TOY 题面

令$dp[i]$为前$i$个装箱的最小花费。
转移方程如下：

用$sum[i]$表示前$i$个容器的长度之和（即$C$的前缀和），方程简化为：

又令$f[i]$为$sum[i]+i$，继续简化方程为：

暴力dp是$O(n^2)$，考虑优化。如何优化，就是用前面所提到的斜率优化。这玩意到底是什么？我们先来继续对状态转移方程进行进一步的推导。

对于每个$dp[i]$可以知道都是由一个$j_0$推过来的。这个$j_0$对于当前的$i$是最优的决策。假设现在有两个决策$j_1,j_2 (1 \leq j_1 < j_2 < i)$，且决策$j_2$优于$j_1$，则有：

拆开可得：

化简可得：

即：

令$g[i] = (f[i]+L+1)^2$，可得：

也就是说，若$j1,j2$满足上面这个式子，那么$j2$一定比$j1$优。

为什么叫斜率优化？因为上面这个式子可以把看作$dp[i]+g[i]$看做纵坐标，$f[i]$看做横坐标，上面的等式右侧就相当于 $\frac{\Delta y}{\Delta x}=k$ 也就是一个一次函数的斜率。当这个斜率$k \leq 2f[i]$则$j_2$优于$j_1$。

假如我们有三个决策$j_1,j_2,j_3$（如下图）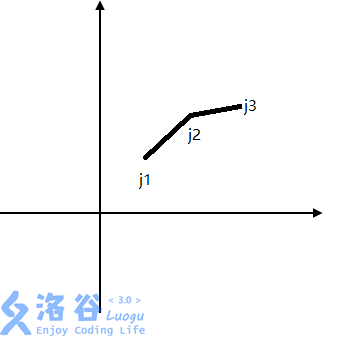

容易证明：$j_2$不可能是最优的。
这样一来，每两个决策间的斜率便是单调上升的。

所以有两种做法：

  • 对于$dp[i]$，有了斜率单调上升这个条件，就可以去二分最优的决策点（也就是斜率小于$2f[i]$的）。复杂度$O(n \log n)$。
  • 又因为$f[i]$是单调递增的，可以用单调队列来维护。具体实现就是，把决策放进一个单调队列里，如果队首和当前的$i$间的斜率 $<f[i]$，就把队首删掉（即h++）。对于队尾，就每次把加入$i$后不满足斜率单调上升的队尾全部删掉（即t—），最后把$i$放进单调队列就好了。

带权二分

先挖个坑。